Computational Fluid Dynamics in Food Processing
- Stelios Chatzidakis

- Jul 1, 2024
- 6 min read
The manufacture of foods involves two broad types of conversions – those concerned primarily with physical changes and those in which irreversible chemical changes are the main purpose of the activity. Regardless of the conversion, ensuring the safety, quality, and shelf-life of food products is paramount. The application of food processing is conducted via conventional or advanced process technologies. Conventional methods involving heating and cooling via indirect systems, namely plate, tubular, and scraped surface heat exchangers, are still the most popular methods used in aseptic processing. Optimization of thermal processing and equipment design requires understanding and solving complex partial differential equations based on fluid motion and heat transfer. One of the cutting-edge tools revolutionizing food processing and manufacturing is the use of Computational Modelling. "Computational models and simulations are a broad and continuously expanding set of basic and advanced tools for simulation, evaluation, optimization, development, and decision-making in a variety of processes, industries, and activities." One vector of Computational Modelling is Computational Fluid Dynamics (CFD) which is the field of study devoted to the solution of equations of fluid flow, heat, and mass transfer with the use of computational methods.
CFD has become the most common method for the initial design, investigation, and testing of new processes and equipment or ways to improve the used processing methods (Yanniotis and Stoforos, 2014; David et al., 2023). Computer simulation is proven to be an alternative to experimentation for gaining a quantitative and qualitative understanding of food process applications. CFD is a simulation modeling tool that can analyze and solve aseptic processing systems' complex fluid flow and heat transfer problems and associated phenomena. The governing equations of fluid flow and heat transfer, known as Navier-Stokes equations, can be considered mathematical formulations of fluid mechanics' conservation laws. CFD comprises the fundamental governing equations of fluid dynamics, involving the solution of the equations of continuity (Eq. 1)), momentum (Eq. 2), and energy (Eq. 3), which are solved numerically to estimate parameters such as velocity, shear, temperature, and pressure profiles inside the system being examined (Yanniotis and Stoforos, 2014).
Continuity or conservation of mass equation describes the overall mass balance within the tube flow:
Where u is the fluid velocity vector (m/s), ρ is the fluid’s density (kg/m^3), and del operator.
The momentum equation describes the motion of fluids. The terms in Eq. 2 correspond to the inertial forces (1), pressure forces (p (Pa)) (2), viscous forces (σ is the stress component (Pa)) (3), and the external forces (F) applied to the fluid (4).
IIn CFD models in the momentum equation, usually the Boussinesq approximation (Eq. 3) is adopted to model density variation caused by buoyancy, based on a reference density (ρref (kg/m^3)) value at a given reference temperature (Tref (K)). However, Boussinesq approximation is not valid when the temperature difference between the evaluated temperature and the reference temperature is high. In this case density can be modeled as:
Finally, the energy equation (Eq. 4) is one of the governing equations applied in aseptic thermal processing CFD modeling. The energy equation (the first law of thermodynamics) describes the rate of energy change of a fluid element, which equals the work done and the heat generated on the element.
Eq. (4) describes the heat transfer in fluids, where cp is the fluid’s specific heat (J/(kg·K)), T is the temperature component (K), and Q describes the external heat sources (W/ m^2).
The solution to the above mathematical set of equations gives the velocity, pressure, and temperature of the fluid at any given point of the modeled domain. The accuracy of the CFD heat transfer problem's solution depends on the input initial and boundary conditions of the problem and the selected structure of the examined domain (Ansys, 2024). Selection of the examined structure (geometry) of the modeled domain directly affects the required time for the solution. The more complex the examined geometry, the longer the simulation time required for the problem to be solved.
Furthermore, the accuracy of the solution of the CFD-heat transfer problem depends on the meshing method and time-step (for unsteady-state problems) selected to solve the problem. Time stepping expresses the frequency of computations in the model. Time-stepping is a critical parameter in time-dependent, unsteady-state problems, where the flow properties are functions of time. In this type of problem, the selection of time-step(s) is critical, and it should be short enough to avoid numerical error(s) and instability of the solution. The selection of the proper time-step applied to the problem depends on the fluid velocity field and the size of the mesh cells applied to the examined domain/geometry. The proper meshing of the examined sub-domains is critical to ensure valid solutions across the common interfaces. For a 3-dimensional model, tetrahedron mesh is more common, while meshes such as quadrilaterals and triangular are typical options for 2-dimensional structures. The governing equations are then discretized and solved inside each of these sub-domains. One of the three following methods is typically used to numerically solve the partial differential equations of the CFD-heat transfer problem: finite volumes, finite elements, and finite differences (Ansys, 2024).
Applications of CFD in Food Processing
Food processing involves multiple stages where fluids play a key role, such as mixing, heating, cooling, and fermenting (Norton and Sun, 2006; Gulati and Datta, 2013; Yanniotis and Stoforos, 2014; David et al., 2023). Preservation methods aim to extend the shelf-life of food while maintaining its safety and quality. CFD models can simulate these processes, offering detailed insights that help optimize operations.
Mixing Efficiency: A uniform mixture is essential for consistency in flavor and texture in food products. CFD can simulate the mixing process, identify dead zones, and suggest equipment or process parameters modifications to ensure homogeneity.
Thermal Processing: Heating and cooling are critical for processes like pasteurization and sterilization. CFD simulations can model the heat transfer within food products and processing equipment, ensuring that target temperatures are reached uniformly and efficiently, enhancing product safety and quality.
Fermentation Control: Fermentation is a key process for products like yogurt, beer, and bread. CFD can help optimize the conditions within fermenters, such as temperature and flow patterns, to ensure optimal microbial activity and product quality.
Refrigeration and Freezing: CFD can model the cooling and freezing processes, ensuring food products reach the desired temperatures.
Packaging Design: Proper packaging is crucial for food preservation. CFD can simulate the behavior of gases within the packaging, helping to design packages that effectively control the exchange of gases like oxygen and carbon dioxide, which are critical for extending shelf-life and maintaining product freshness.
Case Studies and Applications
Several real-world applications of CFD in food processing and safety highlight its importance. The value proposition of CFD is that food extends from heat and mass transfer phenomena such as pasteurization and drying to the deformation that occurs when a kernel is heated, which involves phenomena such as phase change. Some examples are presented below.
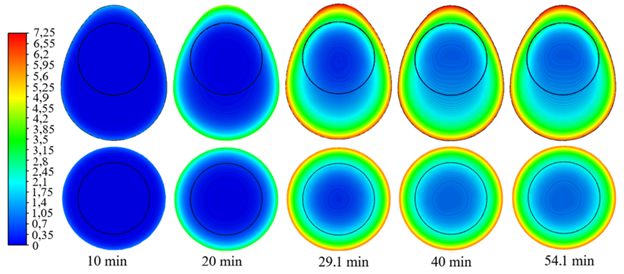
Fig.1: Evolution of the F value distribution, horizontal and vertical cross sections, for the large-size egg during pasteurization (Sampanis et al., 2023).

Fig.2. Fluid Flow in Aseptic processing of liquid and liquid-particulate foods. Below is a video showing the CFD simulation of liquid and liquid-particulate food pipe flow.
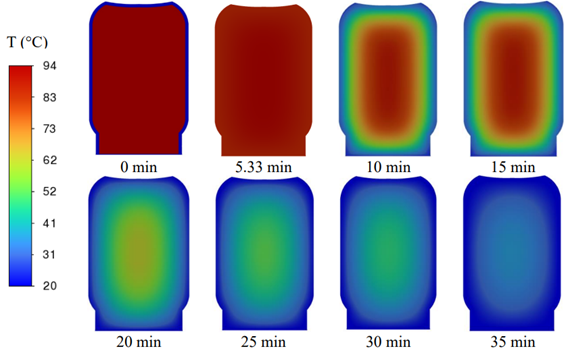
Fig.3: Evolution of temperature distribution during hot fill hold processing of tomato paste (Kourtis, 2023).

Fig.4: Simulated gas pressure with puffing time in rice kernels (Gulati and Datta, 2013).
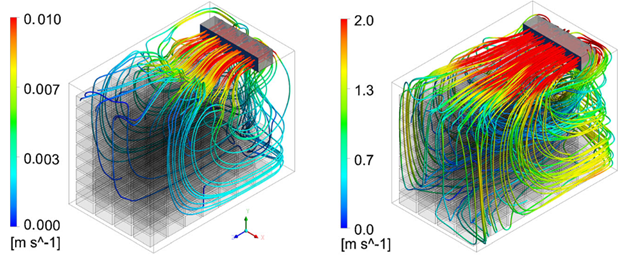
Fig.5: Simulated streamlines of the airflow in wooden bins of Jonagold apple fruit in commercial cooling storage (Ambaw et al., 2013).

Fig.6: Velocity profiles in drying chambers (Cabrera-Escobar et al., 2024).
References
Ambaw, A., Verboven, P., Delele, M. A., Defraeye, T., Tijskens, E., Schenk, A., Nicolai, B. M. (2013). CFD-Based Analysis of 1-MCP Distribution in Commercial Cool Store Rooms: Porous Medium Model Application. Food and Bioprocess Technology, 7(7), 1903-1916. doi:10.1007/s11947-013-1190-9
ANSYS Fluent. (2024). Theory Guide. Ansys Inc.
Cabrera-Escobar, J., Vera, D., Jurado, F., Córdova-Suárez, M., Santillán-Valdiviezo, G., Rodríguez-Orta, A., & Cabrera-Escobar, R. (2024). Optimization of olive pomace dehydration process through the integration of computational fluid dynamics and deep learning. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 46(1), 4756-4776. doi:10.1080/15567036.2024.2331563
David, J. R. D., Coronel, P. M., & Simunovic, J. (2023). Handbook of Aseptic Processing and Packaging. CRC Press.
Gulati, T., & Datta, A. K. (2013). Modeling Flow and Deformation During Hot Air Puffing of Single Rice Kernels.
Kourtis, T. (2023). Modeling the Hot-fill process of tomato juice in glass containers using Computational Fluid Dynamics. MSc Thesis. http://dspace.aua.gr/xmlui/handle/10329/8032 Accessed on June 30, 2024.
Norton, T., & Sun, D. W. (2006). Computational fluid dynamics (CFD) - an effective and efficient design and analysis tool for the food industry: A review. Trends in Food Science & Technology, 17(11), 600-620. doi:10.1016/j.tifs.2006.05.004
Sampanis, P.A., Chatzidakis, S.M., Stoforos, N.G. (2023). Analysis of shell egg pasteurization using Computational Fluid Dynamics. As Presented 14th Panhellenic Scientific Conference on Chemical Engineering.
Yanniotis, S., & Stoforos, N. G. (2014). Modelling food processing operations with computational fluid dynamics: a review. Scientia Agriculturae Bohemica, 45(1), 1-10. doi:10.7160/sab.2014.450101








Comments